お気軽にお問い
解析対象としているモデルの一部寸法を変えるとします。CAE解析があればモデルの寸法を変更し、すぐさま計算を実行することで、応力や変位を素早く確認できます。
しかしながら、このような場合に「おおよそこれくらい結果が変わりそうだ」と頭の中で大体の予測を立てることが簡単にできるケースもあります。
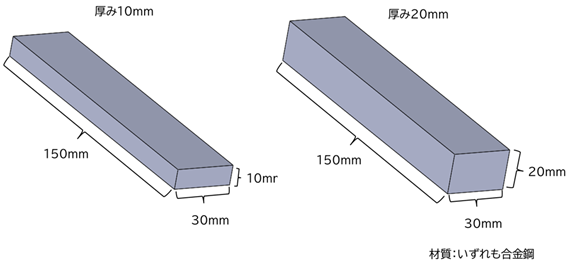
例えば、以下のようなサイズの片持ち梁の曲げをCAE解析で計算してみます。
図1 ： 片持ち梁の形状
曲げ剛性は一般的に、EI （E：ヤング率、I：断面二次モーメント） で表されます。
Eは選択した材料で決まる値です。対してIは断面の形状により決まる値です。つまり剛性は材料と形状の組み合わせにより決まるものであるとわかります。
今回は断面が長方形の梁を想定するので、この場合のIは以下の通りです。
（b：幅、h：厚み）
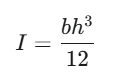
この式からわかることとして、幅方向と厚みを2倍に変えたときの曲げ方向の剛性の変化を考えます。幅方向はbの数値が変化するだけなので、曲げ剛性は2倍変化します。一方で厚みについては3乗になるため、8倍理論上は変わってくるということが計算式から分かります。
また、単純な片持ち梁の曲げを行った際の、たわみ（変形）の最大値の計算式は以下の通りです。剛性を示すEIは分母にあるので、剛性が高いほうがたわみは小さくなります。
（E：ヤング率、I：断面二次モーメント、P：先端集中荷重、L：梁の長さ）
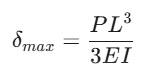
図1で示した片持ち梁は下の図のように、梁の先端に集中荷重（10N）を付加し、片側の側面を完全に拘束して行います。変形状態が示すように、梁の鉛直方向に梁は曲がります。
図2：片持ち梁の解析条件
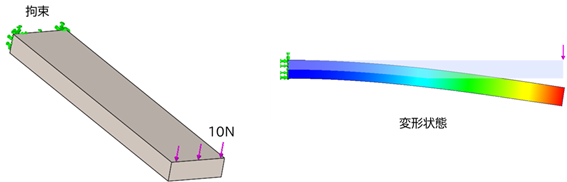
それぞれのモデルの最大変位量は以下の通りになります。
| モデル名 | 最大変位量 |
|---|---|
| 厚み1mm | 0.021mm |
| 厚み20mm | 0.0027mm |
厚み1mmのモデルは厚み20mmのモデルに対して、約7.8倍の最大変位を示しています。曲げ剛性は厚み20mmが厚み10mmのそれに対して約7.8倍であるということであり、先ほどの計算式とほぼ同じ数値になります。0.2倍分、理論式と差がありますが、メッシュ条件をより細かくしていくと、この差はより縮まるかもしれません。
大まかな条件で、ほぼほぼ同じ差異がみられるという認識でここでは大丈夫です。
ここでは、1つのケースについて、断面2次モーメントやたわみの計算式をお出ししています。断面形状や支持される箇所の数や荷重位置によって、これらの式は変化しますので、都度確認しましょう。
