今回は前回のコラムでお話していた内容を補足したいと思います。
前回のコラムでは、梁の厚みが変更された場合の梁の曲げ変形量について、基礎式をもとにその影響を事前に予測することができることをお話ししました。
今回は同じように基礎式をもとに、固有値解析結果を予測することについて触れたいと思います。
固有値解析の結果についても、梁の曲げと類似したモードであれば、同じように基礎式を用いた考え方を生かすことができます。
例えば、梁の先端が曲がる挙動は、固有値解析の1次モードと似ています。
固有値の公式は、1自由度系の場合には次のように定められています。
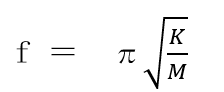
f:固有値(固有振動数)
π:円周率
K:剛性
M:質量
厚みが2倍になるときの曲げ剛性への影響は8倍になると前回お話しをしていました。また、今回は厚みが2倍になるため、Mの部分も2倍となります。
これを上の式に当てはめると、結果的に固有値は2倍になると予想されます。
この曲げの挙動に対する剛性は共通な考え方を当てはめることができるのか、実際に計算結果を見てみます。
前回のコラムと同じモデルではありますが、サイズは以下の通りです。
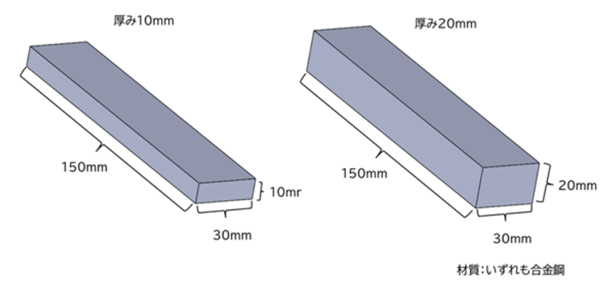
固有値解析の境界条件は以下の通りです。
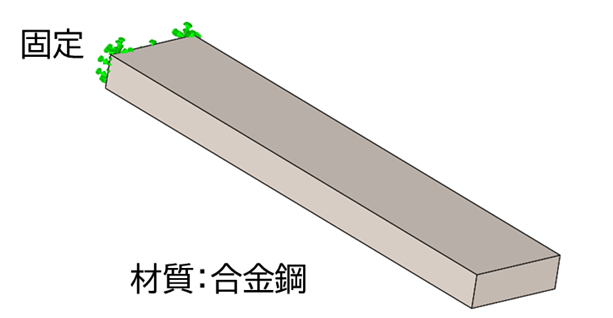
| 厚み10㎜ | 厚み20㎜ | |
|---|---|---|
| 1次モード固有値 | 377Hz | 745Hz |
計算結果を確認すると、厚みが20㎜に変更したあとの固有値は、変更前の745/377≒1.98倍とほぼほぼ2倍となりました。
このように、単純な曲げの変形をするモードに対しては、ある程度、手計算から結果がどれくらい変わるのかを予想ができそうです。
しかしながら、ここでご注意いただきたい点があります。それは、今回あくまで1次モードの単純な梁の変形を題材としているという点です。実際には、1次モードであっても形状によっては、単純な曲げの挙動だけでなく、せん断変形やポアソン効果といった影響も考慮する必要が出てくる場合があり、今回のように予測が難しいケースもございます。また、2次モード、3次モードといった高次なモードになると、変形自体が複雑になるため、今回の基礎式の比率のまま当てはめることは難しい場面があることも念頭に置いていただくと、この方法が使えるケースと使えないケースの線引きができるようになります。








