【構造】製品設計/強度設計の基本講座シリーズ　vol.5　ひずみの定義

2020年09月03日

前回は、４回にわたって「応力」について説明をしてきました。
外力と釣り合っている内力ベクトルを各面に作用している単位面積当たりの表面力として記述したのが応力テンソルでした。

今回からは、「ひずみ」について考えていきたいと思います。
ひずみは、物質の変形によって起こります。変形せず（形が変わらずに）移動だけしてもひずみは発生しません。
最初に、ひずみの定義も含めて、１次元の変形について考えてみます。

ひずみの定義

断面積 $A_{0}$ 、長さ $ｌ_{0}$ の直線棒に軸力Pが作用して、断面積がA、長さが l に変形したとします。
このとき、公称応力S、公称ひずみe と呼ばれるものは、以下で定義されます。
また、真応力σ、真ひずみε（定義から対数ひずみとも呼ばれる）は、以下で定義されます。

応力が単位面積当たりの力（SI単位系でPa）に対して、ひずみは単位長さ当たりの変形量（単位は無次元）となります。
微小変形仮定（変形前後での変形が無限小とみなせる）では、公称ひずみと真ひずみを分ける必要はありませんが、大変形になると真ひずみの定義が必要となってきます。
これは、以下の特性があるためです。

ひずみの加算性

一本の棒が $ｌ_{1}$ -> $ｌ_{2}$ -> $ｌ_{3}$ と２段階に変形したとします。このとき、公称ひずみは加算性が成立しませんが、真ひずみでは成立します。

圧縮ひずみと引張ひずみの等価性

$ｌ_{0}$ - > $ｌ_{1}$ に伸びた場合の引張ひずみと、 $ｌ_{1}$ -> $ｌ_{0}$ に圧縮された場合の圧縮ひずみでは、絶対値が等しくなるはずです。
この時も、公称ひずみは等価性が成立しませんが、真ひずみでは成立します。

微小変形時のひずみの定義

次にYZ面内のひずみを考えてみます。
下図のように、４辺形ABCDの領域が、変形してA’B’C’D’の領域になったとします。

まず、軸方向変形として、辺ABが変形した辺A’B’のY方向の長さ(A’B’)yを考えると、下式になります。
ここで、下線では各辺は線形に伸びるとして、1次の傾きで近似しています。

更に、領域の大きさを無限小にした時、単位長さ当たりの伸び（ひずみ）は、下式で表されることになります。

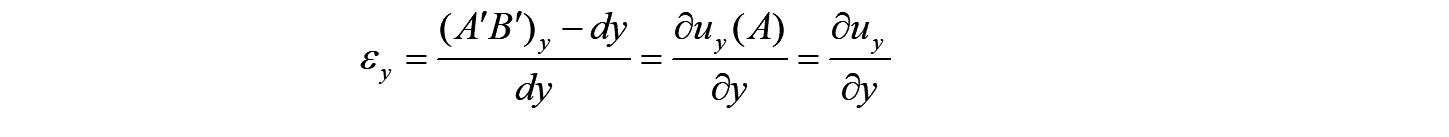
同様に、点Aにおける各方向の軸ひずみは、以下で定義され、工学ひずみと呼ばれます。

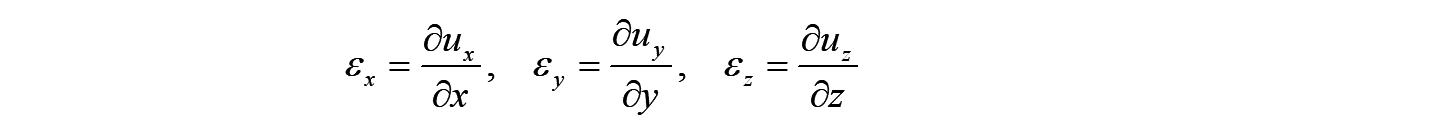
次に、せん断変形を考えます。
線分ABとADの角度変化は、微小変形を仮定すると、下式で表されます。

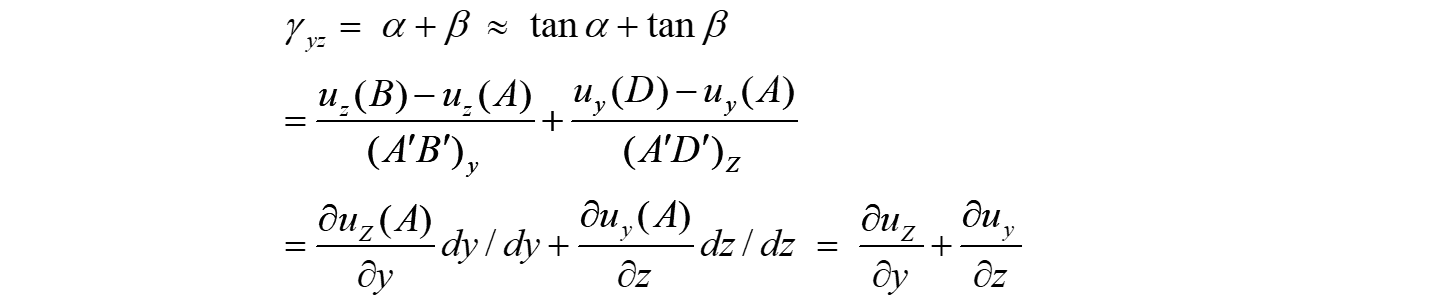
同様に、点Aにおける各方向の角度変化は以下で定義され、工学せん断ひずみと呼ばれます。

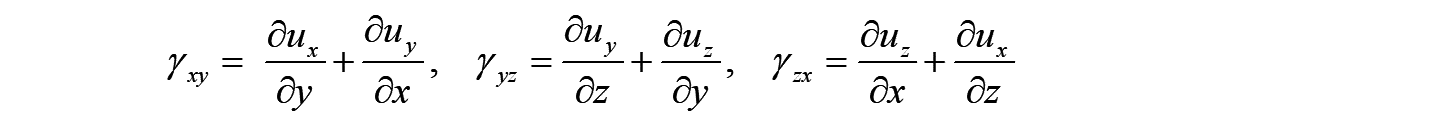
更に、1/2にしたせん断ひずみを定義することにより、以下の３次元でのひずみテンソルが定義できます。
応力テンソルと同様に、ひずみテンソルも対称テンソルとなります。

${du}_{i}$ = $ε_{ij} {dx}_{j}$ の様に、ひずみテンソルは変位ベクトルから変形ベクトルに変換するテンソルであり、変位と変形の関係を示します。
また、モールの応力円と同様に、モールのひずみ円が定義でき、最大主ひずみや最大せん断ひずみで材料強度評価を行うこともあります。

次回は、大変形も考慮したひずみの定義を考えてみます。

[From N. Sahashi]

全体カテゴリ

製品カテゴリ

Topics
トピックス

SBDプロダクツサービス部
SBDエンジニアリング部

技術コラム