COLUMN

技術コラム

【流体】いまさら聞けない熱流体用語Vol.1　レイノルズ数/層流・乱流/カルマン渦

2024年10月01日

この流体コラムでは、『いまさら聞けない熱流体用語』として熱流体の用語を説明します。まずは無次元数（レイノルズ数・プラントル数・ヌセルト数・グラスホフ数など）編です。物理現象は複合的な要因で起き、無次元数と物理現象を一対一対応させた議論は難しいですが、各無次元数と関係性の深い物理現象を例に説明します。

そもそも無次元数の特徴としては、下記が挙げられます
・変数を減らせる、単位系に依存しない式が導ける
・物理量の比として定義され、現象の本質的な特徴を表している
→無次元数を理解することは物理的意味を理解するということにつながります。

レイノルズ数とは

レイノルズ数は粘性効果と慣性効果のバランスを表すものです。
粘性力の影響（流れに抵抗する力）と慣性力の影響（流れを維持しようとする力）の比を取った無次元数です。式に代表長さがあることから分かるように、流体固有の値ではなく流体の流れる環境のスケールの依存性があります。

レイノルズ数は下記の式で表されます。

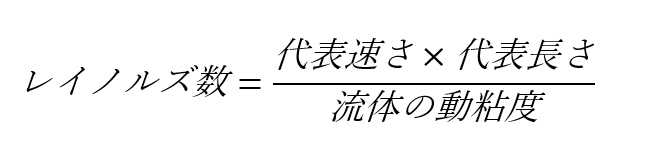
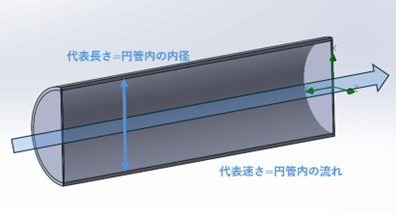
円管内流れの場合の一般的な代表速さと代表長さの取り方は下図の通りです。代表長さ、代表速さのとりかたは基本的に自由です。同じ系について解析を行う場合、代表長さ・距離を揃えることで、異なる解析条件との比較が可能になります。

Fig.1　円管内流れの一般的な代表長さと代表速さの取り方

レイノルズ数はナビエ・ストークス方程式を無次元化することで導出することができます。
レイノルズ数>>1の時、粘性効果が無視でき、オイラー方程式として記述され非粘性流体として扱うことができます。一方、レイノルズ数<<1の時、慣性効果は無視でき、クリープ流またはストークス流れとして記述されます。
このように、レイノルズ数によってナビエ・ストークス方程式を簡略形として扱うことができます。

レイノルズ数の応用

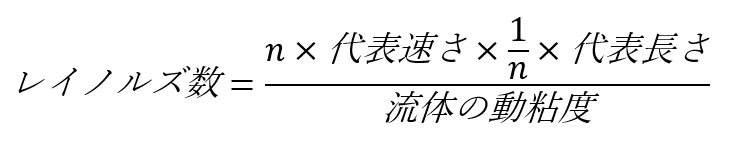
レイノルズ数の式において、代表速さをn倍、代表長さを1/n倍としても同じレイノルズ数となります。すなわち、実物の寸法で作らなくても代表速さをn倍にすれば模型を1/n倍サイズで流れを再現することができます。これをレイノルズの相似則といいます。

詳しくはこちら：【流体】熱と流れの不思議　vol.1　レイノルズの相似則
https://www.sbd.jp/column/wonders_of_flow_vol1_reynolds.html

レイノルズ数と層流・乱流との関係

上記で説明したように、レイノルズ数は簡単にいうと粘性効果と慣性効果のバランスを表すものです。粘性効果が大きい場合、流体の流れに抵抗する形で流れが一体化するかのように安定化し、層流になります。逆に慣性効果が大きい場合では粘りによる流れの一体化の効果に比べて、流れの勢いを維持する効果が大きいため、流れを不安定化し、乱流となります。下表にレイノルズ数と層流・乱流の関係をまとめました。

また、層流と乱流が混在した状態を遷移域、その遷移し始めるレイノルズ数の値を臨界レイノルズ数といいます。レイノルズ数の式からも分かるように流路形状によって代表速度、代表長さが変わるため、ある臨界レイノルズ数を超えているから乱流である、超えていないか層流であるとは決められません。流路形状によって臨界レイノルズ数は異なります。

カルマン渦

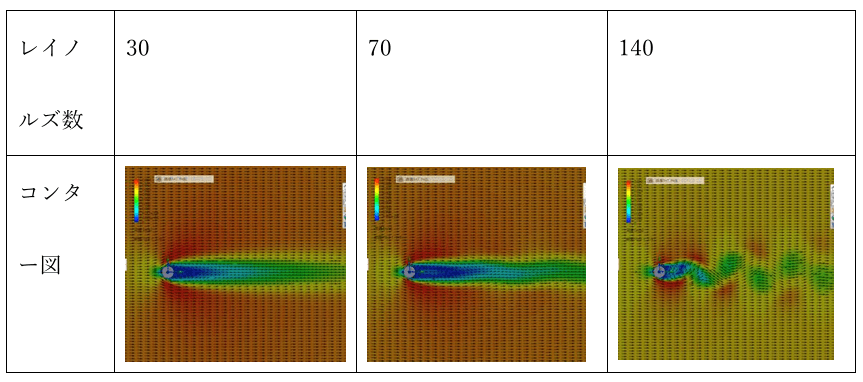
カルマン渦とは物体周りの流れ（今回は円柱）において、ある程度レイノルズ数が大きくなると円柱から剥がれた渦は、円柱下流で一定間隔を保った千鳥状の列を形成します。この渦の列をカルマン渦と呼びます。下図のようなモデルにおいて、代表速さを変更することでレイノルズ数が30、70、140の3つの条件で解析を行いました。

Fig.2　円柱回り流れモデル

下表に小、中、大それぞれのレイノルズ数における流速のコンター図と流跡線をz軸正方向から見た図をまとめました。レイノルズ数を大きくすることでカルマン渦が発生する過程が確認できました。

上表の解析においてはモデルと境界条件は線対称ですが、解析結果として線対称になりません。感覚的に対称な結果になりそうでも対称な結果にならない場合もあります。

解析結果が対称にならないときのヒントはこちら
【流体】熱流体解析スキルアップ講座 Vol.3｜「結果が左右対称になりません」
https://www.sbd.jp/column/flow_improve_skills_vol3.html

余談：血の流れとレイノルズ数

流速と管径が大きい大動脈では血液は常に乱流状態で、一方大動脈の末端以降では管径や流速が小さくなるため層流になります。また、貧血状態では血液の粘度が低下するため、レイノルズ数が大きくなり乱流傾向となります。

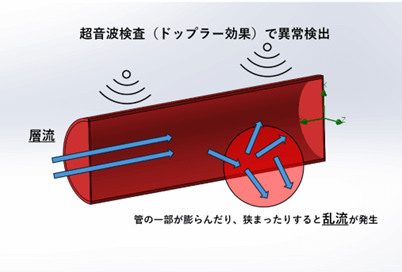
超音波によってドップラー効果で血液の速さや方向を検査することができます。血液の異常流れ（乱流）を検出できます。これは医療診断にも利用されています。下図において矢印は流線を表しています。