構造計画研究所 構造計画研究所 SBDプロダクツサービス部
SBDエンジニアリング部

お気軽にお問い
合わせください

構造計画研究所 構造計画研究所

お問い合わせ

CASE

コネクターの接触解析【3DEXPERIENCE Works Simulation事例】

本事例ではコネクターを対象とし、挿入および抜去の挙動を検証しました。
解析手法として陽解法を使用しました。
本解析によって以下の結果が得られました。
• 挿入および抜去で発生する応力の確認
• 挿入および抜去時に必要なエネルギー量の確認

接触設定

接触の定義：一般接触
一般接触を使用すると、1つの定義でモデル領域内にある多数またはすべての領域間の接触を定義します。
複数の構成部品または複雑なトポロジーを持つモデルに適している手法です。
時刻歴で変化する接触箇所を自動で認識し、精度の良い接触状態を再現します。


解析手法：陽解法

解析手法として陽解法を使用しました。


陽解法
落下や衝突など極めて短い時間に大きなエネルギーが発生する現象の検証に広く利用されている手法です。
義足の鉄球落下試験
衝突試験


陰解法
静解析などで広く利用されている手法です。
ゴムパッキンの強度検証
三点曲げ試験

陰解法と陽解法の違い

手法によりアルゴリズムが違い、それぞれメリットとデメリットがあります。
問題に応じて使い分けることが大事です。

　 　 　 　
陽解法陰解法
アルゴリズム・要素、節点ごとに応力波の伝搬を計算
・未来の状態を現在の状態と既知の情報から直接的に計算する
・慣性力の考慮あり
・収束計算を行わない		 ・モデル全体の釣り合いを計算
・未来の状態を現在の状態も含めて計算する
・慣性力を考慮しない
・釣り合いを保つため収束計算を行う
メリット 非線形性の高い問題でも解を得ることができる 精度の高い結果を得ることができる
デメリット 物理時間により計算時間が長くなる
時間刻みやマススケール設定により精度が悪化する		 非線形性の高い問題では収束解を得るため膨大なパラメータ調整の工数が必要
収束解が得られない場合がある

コネクターモデルの事例における解法の選択

抜去時の山越えが陰解法の鬼門
・陰解法のジレンマ
慣性力の影響にないモデルでは精度の良い陰解法を使用するケースが多いです。ただし、接触など非線形性の高い問題では収束解を得るためにソルバーパラメータの調整が必要となります。特にコネクターの抜去時のような状態が急に変化する計算は収束の難しい事例の1つです。
・陽解法の拡張
陽解法では収束計算を行わないため必ず解を得ることができます。解析精度については慣性力の影響がでないよう動作速度を抑える、エネルギーバランスに注意しながらマススケーリングを利用するなど工夫をすることで、大きな乖離を防ぐことができます。
収束の難しい問題では陽解法の活用がおすすめです。

解析モデルと設定

解析モデルを以下に示します。

解析結果

■　von Mises 応力



■　接触圧力


■　動作負荷

まとめ

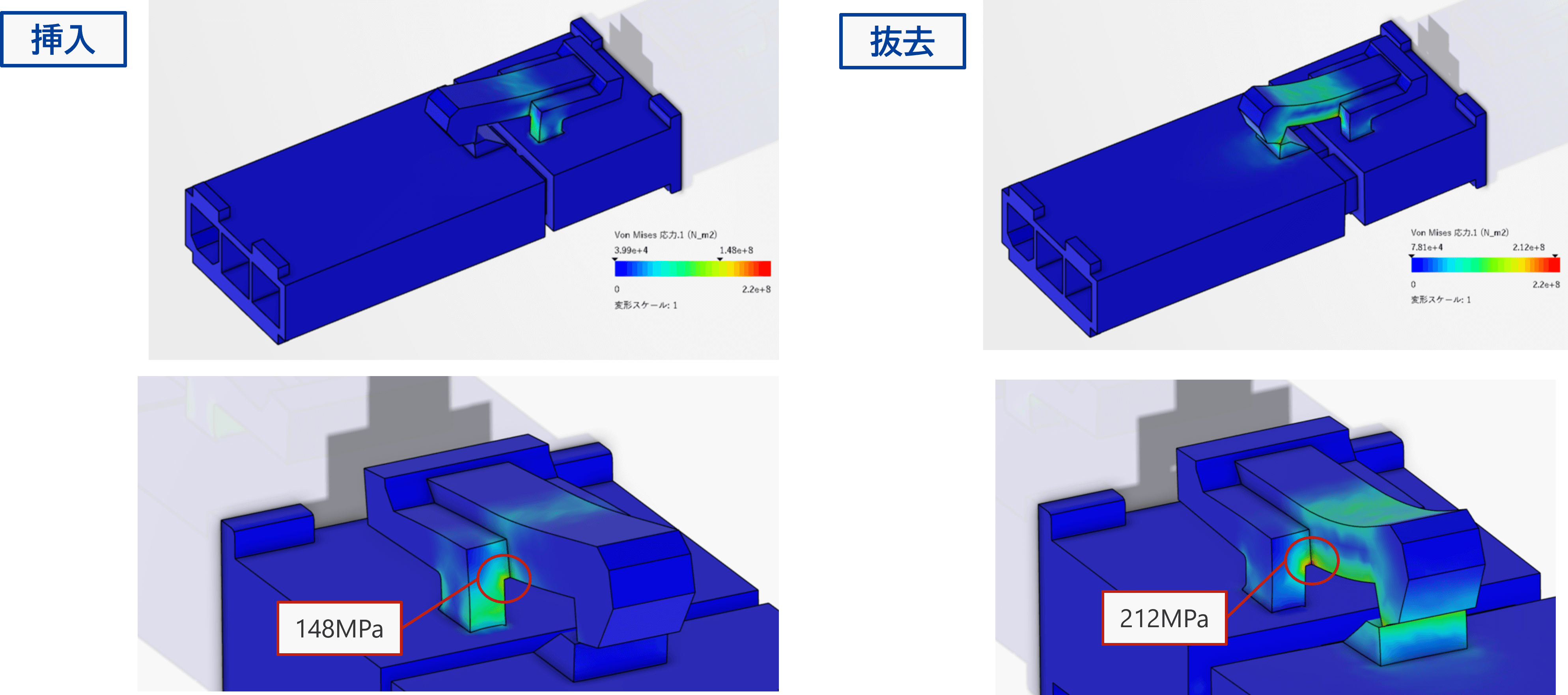
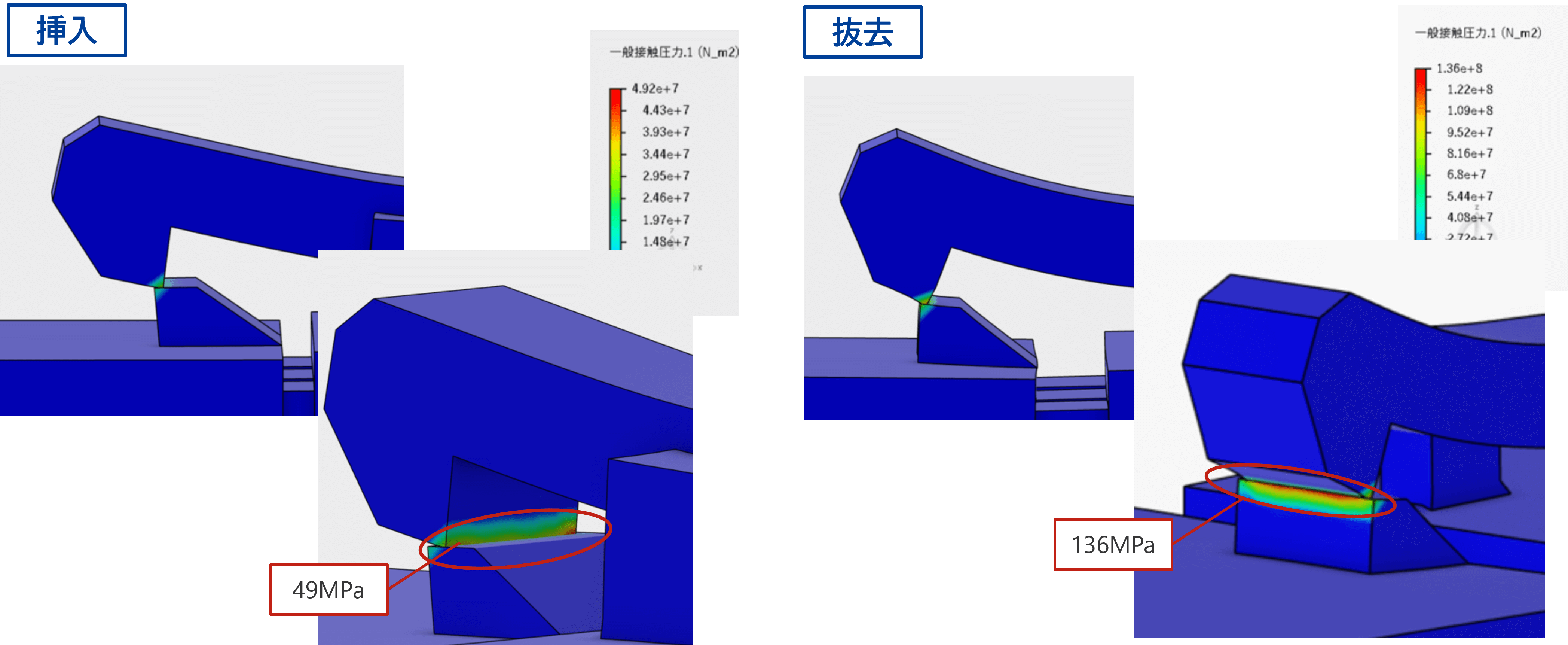
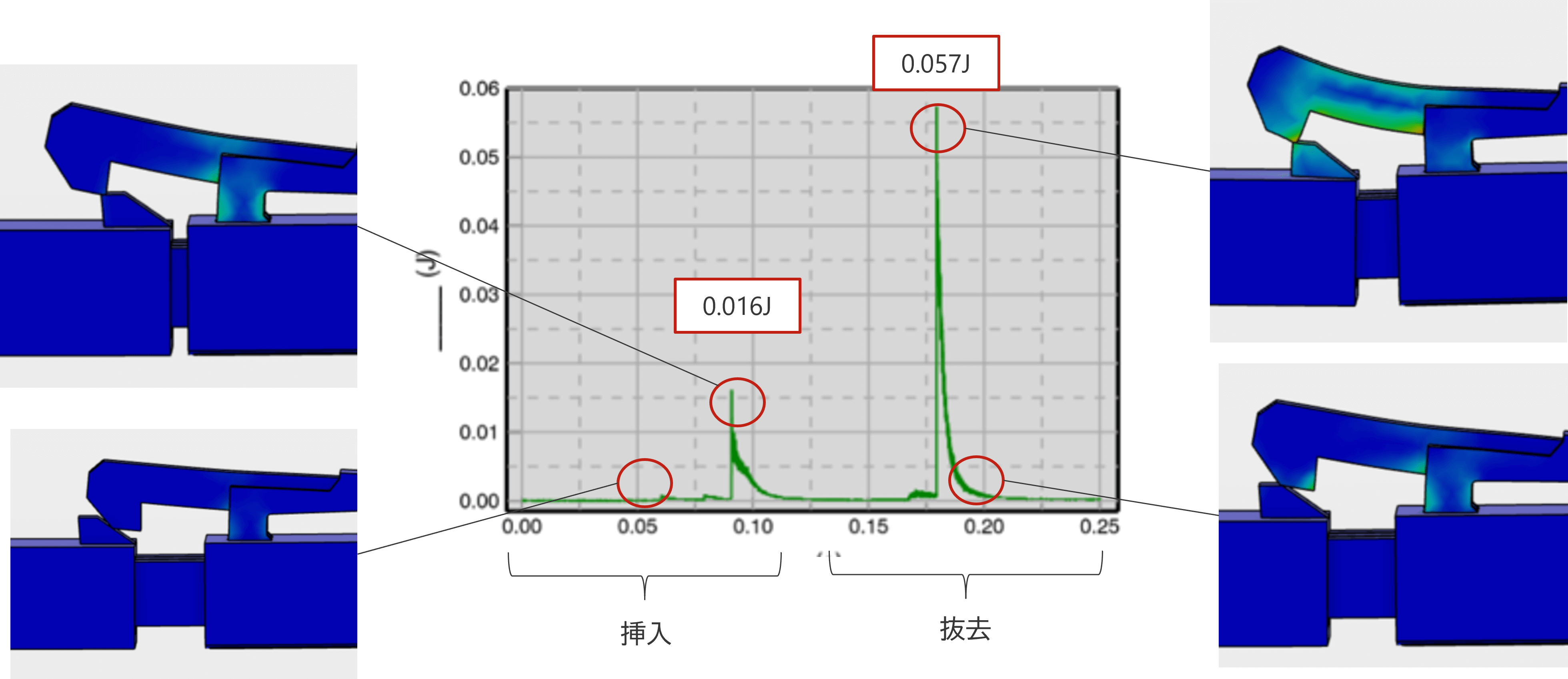
コネクターを対象とし、挿入および抜去の挙動を検証しました。
本解析によって、「挿入および抜去で発生する応力」「挿入および抜去時に必要なエネルギー量」の結果が得られました。
陽解法と陰解法はそれぞれメリットとデメリットがあります。問題に応じて使い分けることが大事です。収束の難しい問題では陽解法の活用がおすすめです。

\

お問い合わせ

3DEXPERIENCE Works Simulation 構造解析　｜　製品ページ

Analysis Case
解析事例

Analysis Case
解析事例

キーワード

もっと詳しい条件で検索する　▼

全体カテゴリ

製品カテゴリ

業種・⽤途

リセット

Topics
トピックス

イベント・セミナー

シミュレーションに関するイベント・セミナー情報をお届けいたします。

もっと見る

トレーニング

SBD製品各種の操作トレーニングを開催しております。

もっと見る

技術コラム

シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。

もっと見る

Topics
トピックス

イベント・セミナー

シミュレーションに関するイベント・セミナー情報をお届けいたします。

もっと見る

トレーニング

SBD製品各種の操作トレーニングを開催しております。

もっと見る

技術コラム

シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。

もっと見る

お問い合わせ

03-5342-1046 受付時間／平日9:00～17:00 お問い合わせフォーム